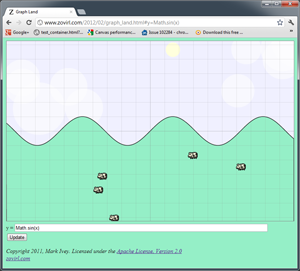
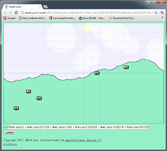
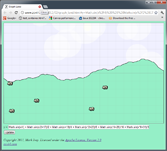
Graph Land: A Graphing Calculator for Javascript, with Cows
Graph Land is a graphing calculator for Javascript. In addition to such useful
features as the ability to plot Math.cos(Math.floor(x*2)), it
also has adorable cows, clouds, dusk, dawn, and other such fine accoutrements
which all fashionable graphing calculators in this modern age aspire toward.
A brief account of the creation of Graph Land
A flight simulator I've been working on needed some interesting terrain for the player to fly over. I saw two solutions: use a level editor to create some interesting terrain (the manual route), or make an algorithm that generates interesting terrain (the procedural route). Making levels by hand is tedious and time-consuming, so I chose procedural terrain generation, which is also time-consuming but more entertaining.
To get rapid feedback while working on the terrain I made a simple app that plotted the output of the algorithm as I tweaked the parameters. It was basically a graphing calculator that took a Javascript expression as input. I used the app to get an algorithm capable of producing convincing hills and mountains, then moved on to work on other things.
Later, I found myself coming back to this app to visualize other things. I used it to tune the length of daytime/nighttime (a modified sine wave) in a different game. Then I needed to smoothly switch colors in another app and I knew the shape of the curve I wanted, but I didn't know what the actual formula was until I messed around in the graphing app for a few minutes and found it.
Much later, cows wandered in. Shortly after that clouds formed in the sky. Eventually the sun, showing no respect for the traditional order of creation by its tardiness, started making a daily appearance.
I've found Graph Land useful. I'm publishing it so others can use it too. The whole thing is licensed under the Apache 2 license, so feel free to reuse it in other projects.
Appendix A
A collection of examples, most of which may be useful to game programmers:
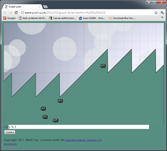
| A) | y = x % 3
| 
|
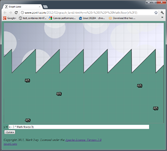
| B) | y = x - 3 * Math.floor(x/3)
| 
|
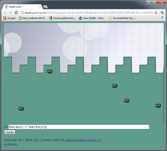
| C) | y = Math.floor(x- 3 * Math.floor(x/3))
| 
|
Javascript's % operator (A) behaves like C not like Python,
which always frustrates me when x is negative. I usually end up
using (B) instead. Rounding down (C) gives a formula that converts any value of
x to a valid index into an array of length 3.
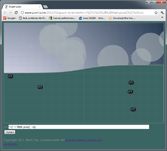
| D) | y = 1/(1 + Math.pow(2, -x))
| 
|
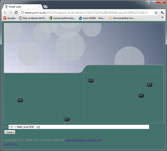
| E) | y = 1/(1 + Math.pow(1000, -x))
| 
|
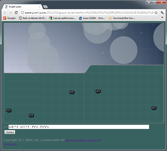
| F) | y = x<0 ? 0 : x>1 ? 1 : 3*x*x - 2*x*x*x
| 
|
Smooth transitions can be down with a modified logistic function (D), which
is very easy to tweak ((A) gives a slow transition, (E) is much more abrupt). A
much faster but less flexible approach is 3x^2-2x^3 (F).
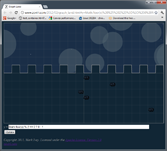
| G) | y = Math.floor(x) % 2 == 0 ? 0 : 1
| 
|
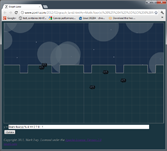
| H) | y = Math.floor(x) % 4 == 0 ? 0 : 1
| 
|
Sometimes you want abrupt transitions, not smooth transitions. (G) and (H) will give you those.
Appendix B
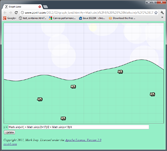
Convincing random terrain is largely a matter of mixing several frequencies together.
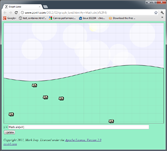
If you use your imagination, you can pretend this is a hill even though it is
too smooth:
y = Math.sin(x/4)
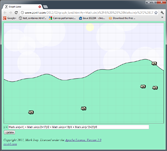
Adding in another higher-frequency, lower-amplitude sine wave makes a
subtle improvement:
y = Math.sin(x/4) + Math.sin(x/2+17)/2
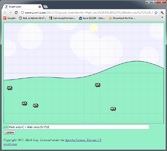
(The "+17" bit offsets the second sine wave so both waves don't cross (0, 0)
together.)
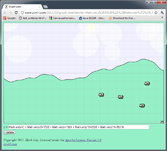
If you keep adding in higher-frequency, lower-amplitude waves you can see the hill gets more and more detail:
The terrain in my flight simulator works the same way except that I use random noise instead of sine waves for the basic input, so instead of combining many layers of sine waves, it is combining many layers of random noise.